Ми живемо в епоху, яка характеризується стрімкими змінами в різних сферах життя суспільства. Поряд з освіченою та фаховою компетентністю особливого значення набувають уміння людини самостійно та нестандартно мислити , висувати нестандартні ідеї та прогнозувати, виявляти творчий підхід у будь-якій діяльності.
Як домогтися розкриття багатству індивідуального світу дитини, що переступила поріг школи? Як організувати навчальний процес пізнання, розвивати творчі здібності учня, щоб в очах малюка не згасав вогник допитливості і навчання стало для нього натхненною захоплюючою працею?
Ось чому питання організації роботи із здібними учнями і створення оптимальних умов для їхньої самореалізації, розкриття творчого потенціалу я розглядаю як одне із приорітетних.
Думка про те, що здібний учень в ході навчання в школі реалізує свої здібності без допомоги вчителя помилкова. Обов'язок кожного вчителя зробити все для того, щоб якнайраніше виявити нахили і здібності учня і допомогти дитині в розвитку її особистості.
Приймаючи учнів-п'ятикласників, проводжу спостереження за роботою учня протягом перших кількох місяців навчання. Відзначаю темп його роботи, зосередженість, сумлінність, зацікавленість в розв'язуванні завдань, запропонованих вчителем. Встановлюю: що дитина любить більше розв'язувати: задачі чи приклади, однотипні чи різні, складні чи легкі, чи любить самостійність у роботі. Наполегливий чи легковажний. Чи замислюється над розв'язком задачі? Чи є спроби знайти різні шляхи розв'язання завдання? Якщо завдання виконане різними способами, то чи відрізняє учень раціональний метод розв'язування від нераціонального.
Звичайно при цьому аналізую психологічний тип характеру дитини: хто він є- холерик чи сангвінік, меланхолік чи проміжний тип. При цьому пам'ятаю, що незалежно від психологічного характеру, кожній людині властиві якісь нахили, здібності, але виявляються вони по-різному.
Перший урок математики у 5-му класі я називаю „ Урок - знайомство". На даному уроці, з метою зацікавлення учнів предметом, проводжу його в ігровій формі. Розв'язуючи завдання на усний рахунок, пропоную учням:
а) задачі-фокуси:
Наприклад: Задумайте число в межах 10. Збільшить його в 4 рази, додайте число , що дорівнює сумі двох задуманих, одержаний результат поділіть на 6, а тоді відніміть задумане число. Я знаю
вашу відповідь: це число 0. Чому?
б) задачі на кмітливість:
1) Як двома відрами 9л і 4л набрати з річки 6л води?
2) є три банки місткістю 8л; 5л; 3л. Восьмилітрова банка наповнена водою. Як відлити в п'ятилітрову банку 4л води?
3) 3 дев'яти однакових монет - одна фальшива, яка відрізняється від інших вагою, проте невідомо, легша вона чи важча. Виявити фальшиву монету трьома зважуваннями на терезах.
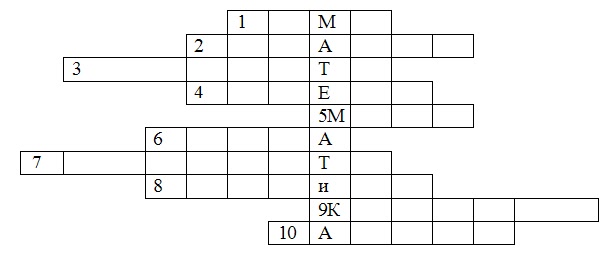
1. Результат дії додавання.
2. Компонент дії додавання.
3. Сума всіх сторін трикутника.
4. Компонент дії ділення.
5. Одиниця вимірювання довжини.
6. Добуток довжини прямокутника на ширину.
7. Сота частина метра.
8. Результат дії віднімання.
9. Чотирикутник, у якого всі сторони рівні.
10. Результат дії ділення.
В ході розгадування цього кросворду виділилось слово „ математика". Наголошую на те, як важливо вчити математику. І неправда, що вона суха і нецікава. Математика і весела і жартівлива, але в той час серйозна і вимоглива.
І так урок за уроком ввожу п'ятикласників у світ математичних знань. Цілком переконана, що тільки тоді можна розвивати творчі здібності учнів, якщо вони добре будуть орієнтуватися у програмовому
матеріалі. З цією метою, починаючи з п'ятого класу привчаю дітей читати підручник, вміти знайти те основне в тексті, що учні повинні запам'ятати, орієнтуватися у знаходженні того, що забув, у підручнику.
Учням-п'ятикласникам часто даю задачі-жарти, що спонукають до логічного мислення, розвитку уваги і швидкості обчислень.
Наприклад: Копав Івась картоплю. Та швидко він копав: за кожні півгодини сім відер набирав. Попрацював він п'ять годин, пішов відпочивати. Так скільки встиг картоплі Іванко накопати?
(70 відер).
Або: Один старий господар відвіз у млин зерно. Молов він дві години, лиш три мішки змолов, а треба все ж змолоти. Ще через шість годин залишився у нього з зерном мішок один. Скільки ж мішків зерна повіз до млина господар?
(13 мішків).
Або: У Вінні- Пуха було 42кг меду. Він з'їдає по 2 банки щодня, а кожна містить 600г меду. Допоможи Віні-Пуху підрахувати, скільки в нього залишилося меду, якщо він їсть його вже 18 днів.
(20кг 400г).
Вивчаючи тему „ Натуральні числа та дії ними" часто практикую як математичну розминку на початку уроку завдання типу:
1) . Як записати число 10, використовуючи п'ять однакових цифр, сполучивши їх знаками дій? Навести кілька варіантів відповіді.
(2+2+2+2+2; 3+3+3+3:3 та ін.)
2) . Як записати число 1 трьома різними цифрами , поставивши між ними знак „-". Навести кілька прикладів:
(7-4-2=1; 7-5-1=1; 6-4-1=1 і ін.)
3) . Добуток яких чотирьох натуральних чисел дає 20?
(5*2*2*1=20; 5*4*1*1=20 і ін.)
Для домашньої роботи завдання даються дещо складніші , які потребують затрати більше часу на їх розв'язування, та нестандартного підходу при їх розв'язуванні. Наприклад:
1). Розставити у записі 4*12+18:6+3 дужки так, щоб утворилося :
а) число 50;
б) найменше можливе число;
в) найбільше можливе число.
2). Скільки існує різних трицифрових натуральних чисел. Знайти їх суму.
Трицифрових чисел -900.
(999+100)+(998+101 )+(997+102)+... *450= 1099*450=494550
Одним із завдань освіти є формування творчої особистості, але у класі не всі діти мають однакові здібності, а ми повинні розвивати їх у кожного учня і на кожному уроці.
З цією метою досить часто використовую тестову перевірку знань учнів, яка сприяє перевірці програмового матеріалу та розвитку логічного мислення.
Наприклад, вивчаючи тему „ Площа квадрата " (5 кл) даю тести: Чи вірні твердження:
1) . Чотирикутник, у якого всі кути прямі, називається прямокутником?
а) так б) ні
2) . Чотирикутник, у якого всі сторони рівні називається квадратом?
а) так б) ні
3) . Чи можна назвати довільний прямокутник квадратом?
а) так б) ні
4) . Чи можна назвати довільний квадрат прямокутником?
а) так б) ні
5) . Чи можна обчислити периметр квадрата за формулою периметра прямокутника ?
а) так б) ні
6) . Чи можна обчислити периметр довільного прямокутника за формулою периметра квадрата?
а) так б) ні
7) . Чи вірно, що площа прямокутника дорівнює добутку довжини на ширину прямокутника?
а) так б) ні
Значне місце в розвитку творчих здібностей учнів приділяю розв'язуванню задач різними способами. Розв'язувати задачі різними способами привчаю поступово, починаючи із 6-го класу.
В класі задачу в більшості розв'язуємо одним або двома способами. Пошук інших способів розв'язування дається додому, при цьому вказую, які теореми можна використати при розв'язуванні. Інколи знайдені
учнями способи розв'язування тієї чи іншої задачі бувають досить громіздкими, складними, але для навчальної і виховної мети така робота досить важлива: діти з цікавістю знаходять шляхи розв'язку задачі, перебираючи в пам'яті багато варіантів застосування вивченого матеріалу, відомих прийомів і методів розв'язування задач.
учнями способи розв'язування тієї чи іншої задачі бувають досить громіздкими, складними, але для навчальної і виховної мети така робота досить важлива: діти з цікавістю знаходять шляхи розв'язку задачі, перебираючи в пам'яті багато варіантів застосування вивченого матеріалу, відомих прийомів і методів розв'язування задач.
Цілком впевнена, що при підсумковому повторенні будь-якого розділу програми доцільно використовувати задачі, що розв'язуються декількома способами, і що охоплюють великий теоретичний матеріал.
Систематична, планомірна і наполеглива робота вчителя у формуванні в учнів навиків у знаходженні різних способів розв'язування задач сприяє розвитку прийомів логічного пошуку, який, в свою чергу, розвиває творчі здібності учнів.
Розглянемо розв'язок декількома різними способами планіметричних задач із навчального посібника А.В. Погорєлова „ Геометрія 7-11".
§4. №46.
Висоти трикутника АВС, проведенні з вершин А і С перетинаються в точці М. Знайти <АМС, якщо
I спосіб розв'язування:
Із прямокутних трикутників АКС і АNС
випливає, що < КСА=90°-70°=20°, <NАС = 90о-80°=10°, тоді <АМС= 180о-(20°+10о)=150°.
II спосіб розв'язування:
Обчислимо < АВС=180°-(70о+80о)=30°.
Визначимо <КСВ=90о-30°=60°,
а тоді <NМС=90°-60°=30°, а він є суміжним із кутом АМС. Звідси <АМС=180о-30°=150°.
9 кл. Тема „ Площі фігур".
Задача: Периметр прямокутного трикутника 60см. Висота проведена до гіпотенузи дорівнює 12см. Знайти площу трикутника
I спосіб.
Знаючи, що SABC =1/2Pr маємо, = 30 –c
Отже SABC = 30 * ( 30 – c)
З іншої сторони SABC = ½ c * h = ½ * 12 *c= =6c.
с+5с=150
6с=150,де 6c=SABC=150 см2.
II спосіб
За теоремою Піфагора а2+Ь2=с2. Площу трикутника АСВ можна знайти:
S = ½ ab, або S = ½ ch
Звідси випливає, що ½ab = 1/2ch, або а*Ь=с*h=12*с. Знаючи, що а+Ь+с=60, маємо, що (а+Ь)=60-с, а звідси (а+Ь)2=(60-с)2
а2+2аЬ+Ь2=3600-120с+с2, де а2+Ь2=с2. Маючи, що а*Ь=12*с, одержимо: 24*с=3600-120*с
144*с=3600
с=25.Отже, S ABC = 1/2*25*12=150
Площу трикутника АСВ знайдемо за формулою:
5ABC=1/2*с*h=1/2*12*с=6*с.
З іншої сторони
S ABC = ½ *p * r = 30 * r, звідси
6*с=30*г,
а с=5*г
ІІІ спосіб
Використовуючи властивість відрізків дотичних, проведених з точки поза колом маємо: г+m+с+г+n=60 або 2*г+2*с=60. Отже: г+с=30, або г+5*г=30, де г=5см. Знаючи
радіус вписаного кола, можна знайти площу а АСВ:
SABC = 30*5 = 150cм2
Особливо вражає учнів нестандартне розв'язування стандартних вправ.
Нехай дано рівняння:
Його легко можна розв'язати, звівши до дробово-раціонального рівняння. Але це рівняння має й інше нестандартне розв'язування: 3 і  - корені очевидні. Але якщо розглянути друге рівняння, то цей прийом побачити значно складніше.
- корені очевидні. Але якщо розглянути друге рівняння, то цей прийом побачити значно складніше.
 - корені очевидні. Але якщо розглянути друге рівняння, то цей прийом побачити значно складніше.
- корені очевидні. Але якщо розглянути друге рівняння, то цей прийом побачити значно складніше.
Якщо учні не зможуть знайти нестандартний розв'язок цього рівняння, то доцільно їм показати, що із рівняння
то цей прийом побачити значно складніше. Якщо учні не зможуть знайти нестандартний розв'язок цього рівняння, то доцільно їм показати, що із рівняння
звідки:
Такі прийоми розв'язування розвивають в учнів гнучкість, оригінальність, нешаблонність мислення, розвивають творчість.
Німецький психолог Фромм казав, що творчість - „це здатність дивувати і пізнавати, вміння знаходити рішення в нестандартних ситуаціях»
Наведу приклади, які сприяють розвитку творчого мислення на уроках алгебри в середній школі.
На уроках вчитель працює з учнями різних ступенів підготовленості. Тому для індивідуальної роботи з більш здібними до математики учнями не завжди є час. Для такої роботи в основному використовуються різні види позакласних занять. Одним з таких видів занять - факультативні заняття, де основною задачею передбачаю: як можна повніше розкрити потенціально творчі здібності кожного учня, що відвідує факультатив.
Не секрет, що багато учнів не вміють довго розумово працювати. При розв'язуванні задач практично все зводиться до реалізації загальної схеми: на обчислення, пояснення і оформлення. Так що заняття факультативів повинні перш за все вчити знаходити ідею розв'язку задачі, не забуваючи удосконалювати і технічну підготовку учнів (виконувати складні обчислення, алгебраїчні перетворення і ін.).
На заняттях факультативу знайомлю учнів із різними типами нестандартних задач, а саме:
а) на відшукання простих закономірностей;
б) на застосування відомих математичних положень в нових умовах;
в) задачам, які нібито можна розв'язати вже відомими способами, але детальний аналіз показує, що треба шукати інші методи розв'язування;
г) на відшукання умов, при яких можуть існувати математичні об'єкти.
Наприклад:
1) Число починається цифрою 4. Якщо цю цифру переставити з першого на останнє місце, то число, яке ми дістанемо буде в 4 рази менше за дане. Чи існує таке число?
2) Один чотирикутник міститься всередині другого. Чи може сума діагоналей внутрішнього чотирикутника бути більшою, ніж сума діагоналей зовнішнього?
Значний ефект дає розв'язування задач, що вимагають від учнів узагальнень конкретних умов. Наведу приклади таких задач:
Задача 1. Дослідити, яку фігуру дістанемо, якщо з'єднаємо відрізками середини послідовних сторін трапеції.
Задача 1а. В якому випадку цією фігурою буде ромб? прямокутник?
Задача 2. Сторони трикутника 20, 28 і 34 см. Визначити вид трикутника (відносно кутів).
Задача 2а. Як треба змінити умову задачі, щоб трикутник був прямокутним? В яких межах може змінюватися сторона, щоб трикутник залишався гострокутним?
Задача 3. Розв'язати рівняння:
Задача За. Чи можна використати знайдений розв'язок для розв'язування рівняння:
tg3х+tg6х=tg9х ?
Велику увагу на заняттях факультативу звертаю на розв'язування завдань з модулями та параметрами.
Учні, знаючи що модуль числа виражається завжди значенням невід'ємним, повинні перш за все вміти розкрити модуль, і визначити, на якій множині вираз, що стоїть під знаком модуля є додатним або від'ємним.
Так після вивчення теми „ Лінійна функція, її графік і властивості" (8 кл.) на заняттях факультативу розглядаємо, як побудувати графіки таких функцій:
а) у= х|;
б)у=|х-1|+|х+2|;
в) |у|=2х+3;
г)у=|2|х|-1|
а після вивчення теми "Квадратична функція" (9 кл.) будуємо слідуючі графіки:
а) у=х2-|х|-6;
б) у=|х2-5х+6|;
в) у=|х2-2|х|-8|
та інші.
Однією із найскладніших для сприйняття учнями тем шкільного курсу математики є розв'язування рівнянь, систем рівнянь і нерівностей з параметрами.
Починаючи із сьомого класу ознайомлюю учнів з найпростішими рівняннями, що містять параметри безпосередньо на уроках. Проте завдання більш складніші з параметрами розглядаються на факультативах.
Наприклад:
7 кл.
1) Розв'язати рівняння:
а2х=а(х+2)-2
2) для яких натуральних значень параметра а рівняння
ах=а+х+1
має парні корені?
8 кл.
1) Розв'язати рівняння:
2) для яких значень параметра а прямі
2х+у=1 і Зах-2у=4
перетинаються.
9 кл.
Знайти всі значення параметра а, для яких прямі
4х-3у-а=0 і 5х-ау+8=0 перетинаються в точці з від'ємними координатами.
І так, розглядаючи поступово завдання з параметрами (рівняння, системи, нерівності), учні можуть розв'язати такі завдання і в старших класах.
Значне місце на заняттях факультативу займають завдання на теми:
І. Тема: Подільність чисел.
Наприклад:
1) Довести, що n3 – n ділиться на 6, якщо n - ціле число.
2) Сума трьох цілих чисел ділиться на 6. Довести, що і сума кубів цих чисел ділиться на 6.
3) Знайти остачу від ділення
4343-1717 на 10.
4) Довести, що при будь-якому цілому п
п6+2п5-п2-2п
ділиться на 120.
II. Тема: Цілі розв'язки.
Наприклад:
III. Тема: Нерівності.
Наприклад:
IV. Квадратний тричлен.
Наприклад:
1) Не знаходячи коренів квадратного рівняння ах2+х-2=0 визначити, при яких значеннях параметра а різниця коренів дорівнює 3.
2) Для яких дійсних значень параметра а рівняння
(а-2)х2-2(а+3)х+4а=0
має один корінь, який більший за 3, а другий менший від 2?
Перелічені питання не вичерпують усього того, що може і повинен робити вчитель для розвитку математичних здібностей учнів.
Творчий підхід до справи, постійні пошуки нового, систематична робота над підвищенням своєї педагогічної майстерності і фахового рівня є вирішальними у цій справі, як і в усіх інших питаннях навчання і виховання підростаючого покоління.
Добре організована позакласна робота з математики є найдійовішим засобом розвитку здібностей учнів. Розв'язування цікавих задач на заняттях факультативу виховує сумлінне ставлення учнів до навчання, вміння долати труднощі і не впадати в розпач в разі невдачі.
Творчий дослідницький характер математичних завдань більш ніж що інше, сприяє росту і зміцненню інтелекту учня. Хто хоч раз пізнав радість творчого досягнення, той ніколи вже не пожалкує зусиль, щоб знову цю радість відчути.
h
h
|












Немає коментарів:
Дописати коментар